ItsMyCode: Calculate Euclidean Distance in Python

In this article, we will be using the NumPy and SciPy modules to Calculate Euclidean Distance in Python.

In mathematics, the Euclidean Distance refers to the distance between two points in the plane or 3-dimensional space. In short, we can say that it is the shortest distance between 2 points irrespective of dimensions.

How to Calculate Euclidean Distance in Python?

The formula to calculate the distance between two points (x1 1 , y1 1 ) and (x2 2 , y2 2 ) is d = √[(x2 – x1)2 + (y2 – y1)2].

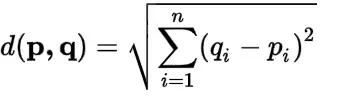Euclidean Distance Formula

There are 4 different approaches for finding the Euclidean distance in Python using the NumPy and SciPy libraries.

1. Using linalg.norm()
2. Using dot() and sqrt()
3. Using square() and sum() 
4. Using distance.euclidean() from SciPy Module

Method 1: Using linalg.norm() Method in NumPy

The NumPy module has a norm() method, which can be used to find the required distance when the data is provided in the form of an array.

The norm() method returns the vector norm of an array. You can learn more about the linalg.norm() method here.

Example

# Python code to find Euclidean distance
# using linalg.norm()

# Import NumPy Library
import numpy as np

# initializing points in
# numpy arrays
point1 = np.array((4, 4, 2))
point2 = np.array((1, 2, 1))

# calculate Euclidean distance
# using linalg.norm() method
dist = np.linalg.norm(point1 - point2)

# printing Euclidean distance
print(dist)

Output

3.7416573867739413

Method 2: Using dot() and sqrt() methods

We can leverage the NumPy dot() method for finding the dot product of the difference of points, and by doing the square root of the output returned by the dot() method, we will be getting the Euclidean distance. 

# Python code to find Euclidean distance
# using dot() and sqrt() methods

# Import NumPy Library
import numpy as np

# initializing points in
# numpy arrays
point1 = np.array((4, 4, 2))
point2 = np.array((1, 2, 1))

# subtracting both the vectors
temp = point1 - point2
 
# Perform dot product
# and do the square root
dist = np.sqrt(np.dot(temp.T, temp))
 
# printing Euclidean distance
print(dist)

Output

3.7416573867739413

Method 3: Using square() and sum() methods

Another alternate way is to apply the mathematical formula (d = √[(x2 – x1)2 + (y2 – y1)2]) using the NumPy Module to Calculate Euclidean Distance in Python

The sum() function will return the sum of elements, and we will apply the square root to the returned element to get the Euclidean distance.

# Python code to find Euclidean distance
# using square() and sum() methods

# Import NumPy Library
import numpy as np

# initializing points in
# numpy arrays
point1 = np.array((4, 4, 2))
point2 = np.array((1, 2, 1))

# finding sum of squares
sum_vectors = np.sum(np.square(point1 - point2))
 
# perform the squareroot and
# print Euclidean distance
print(np.sqrt(sum_vectors))

Output

3.7416573867739413

Method 4: Using distance.euclidean() from SciPy Module

We discussed several methods to Calculate Euclidean distance in Python using the NumPy module. These methods can be slower when it comes to performance, and hence we can use the SciPy library, which is much more performance efficient.

The SciPy module is mainly used for mathematical and scientific calculations. It has a built-in distance.euclidean() method that returns the Euclidean Distance between two points.

# Python code to find Euclidean distance
# using distance.euclidean() method

# Import SciPi Library
from scipy.spatial import distance

# initializing points in
# numpy arrays
point1 = (4, 4, 2)
point2 = (1, 2, 1)
 
# print Euclidean distance 
print(distance.euclidean(point1,point2))

Output

3.7416573867739413

from Planet Python
via read more