Python for Beginners: Binary Search Tree in Python

You can use different data structures such as a python dictionary, a list, a tuple, or a set in programs. But these data structures are not sufficient for implementing hierarchical structures in the programs. In this article, we will study about binary search tree data structure and will implement them in python for better understanding. 

What is a Binary Tree?

A binary tree is a tree data structure in which each node can have a maximum of 2 children.  It means that each node in a binary tree can have either one, or two or no children. Each node in a binary tree contains data and references to its children. Both the children are named as left child and the right child according to their position. The structure of a node in a binary tree is shown in the following figure.

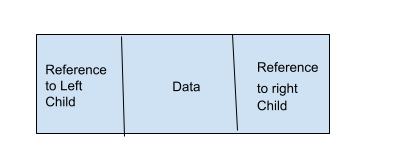Node of a Binary Tree

We can implement a binary tree node in python as follows.

class BinaryTreeNode:
  def __init__(self, data):
    self.data = data
    self.leftChild = None
    self.rightChild=None

What is a Binary Search Tree?

A binary search tree is a binary tree data structure with the following properties.

• There are no duplicate elements in a binary search tree.
• The element at the left child of a node is always less than the element at the current node.  
• The left subtree of a node has all elements less than the current node.
• The element at the right child of a node is always greater than the element at the current node.
• The right subtree of a node has all elements greater than the current node. 

Following is an example of a binary search tree that satisfies all the properties discussed above.

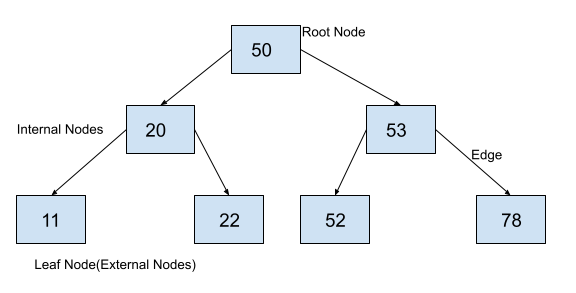Binary search tree

Now we will implement some of the basic operations on a binary search tree.

How to Insert an Element in a Binary Search Tree?

We will use the properties of binary search trees to insert elements into it. If we want to insert an element at a specific node, three conditions may arise.

1. The current node can be an empty node i.e. None. In this case, we will create a new node with the element to be inserted and will assign the new node to the current node.
2. The element to be inserted can be greater than the element at the current node. In this case, we will insert the new element in the right subtree of the current node as the right subtree of any node contains all the elements greater than the current node.
3. The element to be inserted can be less than the element at the current node. In this case, we will insert the new element in the left subtree of the current node as the left subtree of any node contains all the elements lesser than the current node.

To insert an element, we will start from the root node and will insert the element into the binary search tree according to the above defined rules. The algorithm to insert elements in a binary search tree is implemented as in Python as follows.

class BinaryTreeNode:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None


def insert(root, newValue):
    # if binary search tree is empty, create a new node and declare it as root
    if root is None:
        root = BinaryTreeNode(newValue)
        return root
    # if newValue is less than value of data in root, add it to left subtree and proceed recursively
    if newValue < root.data:
        root.leftChild = insert(root.leftChild, newValue)
    else:
        # if newValue is greater than value of data in root, add it to right subtree and proceed recursively
        root.rightChild = insert(root.rightChild, newValue)
    return root


root = insert(None, 50)
insert(root, 20)
insert(root, 53)
insert(root, 11)
insert(root, 22)
insert(root, 52)
insert(root, 78)
node1 = root
node2 = node1.leftChild
node3 = node1.rightChild
node4 = node2.leftChild
node5 = node2.rightChild
node6 = node3.leftChild
node7 = node3.rightChild
print("Root Node is:")
print(node1.data)

print("left child of the node is:")
print(node1.leftChild.data)

print("right child of the node is:")
print(node1.rightChild.data)

print("Node is:")
print(node2.data)

print("left child of the node is:")
print(node2.leftChild.data)

print("right child of the node is:")
print(node2.rightChild.data)

print("Node is:")
print(node3.data)

print("left child of the node is:")
print(node3.leftChild.data)

print("right child of the node is:")
print(node3.rightChild.data)

print("Node is:")
print(node4.data)

print("left child of the node is:")
print(node4.leftChild)

print("right child of the node is:")
print(node4.rightChild)

print("Node is:")
print(node5.data)

print("left child of the node is:")
print(node5.leftChild)

print("right child of the node is:")
print(node5.rightChild)

print("Node is:")
print(node6.data)

print("left child of the node is:")
print(node6.leftChild)

print("right child of the node is:")
print(node6.rightChild)

print("Node is:")
print(node7.data)

print("left child of the node is:")
print(node7.leftChild)

print("right child of the node is:")
print(node7.rightChild)

Output:

Root Node is:
50
left child of the node is:
20
right child of the node is:
53
Node is:
20
left child of the node is:
11
right child of the node is:
22
Node is:
53
left child of the node is:
52
right child of the node is:
78
Node is:
11
left child of the node is:
None
right child of the node is:
None
Node is:
22
left child of the node is:
None
right child of the node is:
None
Node is:
52
left child of the node is:
None
right child of the node is:
None
Node is:
78
left child of the node is:
None
right child of the node is:
None

How to search an element in a Binary search Tree?

As you know that a binary search tree cannot have duplicate elements, we can search any element in a binary search tree using the following rules that are based on the properties of the binary search trees. We will start from the root and follow these properties

1. If the current node is empty, we will say that the element is not present in the binary search tree.
2. If the element in the current node is greater than the element to be searched, we will search the element in its left subtree as the left subtree of any node contains all the elements lesser than the current node.
3. If the element in the current node is less than the element to be searched, we will search the element in its right subtree as the right subtree of any node contains all the elements greater  than the current node.
4. If the element at the current node is equal to the element to be searched, we will return True.

The algorithm to search an element in a binary search tree based on the above properties is implemented in the following program. 

class BinaryTreeNode:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None


def insert(root, newValue):
    # if binary search tree is empty, create a new node and declare it as root
    if root is None:
        root = BinaryTreeNode(newValue)
        return root
    # if newValue is less than value of data in root, add it to left subtree and proceed recursively
    if newValue < root.data:
        root.leftChild = insert(root.leftChild, newValue)
    else:
        # if newValue is greater than value of data in root, add it to right subtree and proceed recursively
        root.rightChild = insert(root.rightChild, newValue)
    return root


def search(root, value):
    # node is empty
    if root is None:
        return False
    # if element is equal to the element to be searched
    elif root.data == value:
        return True
    # element to be searched is less than the current node
    elif root.data > value:
        return search(root.leftChild, value)
    # element to be searched is greater than the current node
    else:
        return search(root.rightChild, value)


root = insert(None, 50)
insert(root, 20)
insert(root, 53)
insert(root, 11)
insert(root, 22)
insert(root, 52)
insert(root, 78)
print("53 is present in the binary tree:", search(root, 53))
print("100 is present in the binary tree:", search(root, 100))

Output:

53 is present in the binary tree: True
100 is present in the binary tree: False

Conclusion

In this article, we have discussed binary search trees and their properties. We have also implemented the algorithms to insert elements into a binary search tree and to search elements in a binary search tree in Python. To learn more about data structures in Python, you can read this article on Linked list in python.

The post Binary Search Tree in Python appeared first on PythonForBeginners.com.

from Planet Python
via read more