Ned Batchelder: Letter boxed

With more time on my hands during this quarantine time, I started doing the Letter Boxed puzzle. You are given a square with three letters on each side:

You form words by choosing letters in sequence. The only rule is that the next letter must be on a different side of the square than the previous letter:

Your next word has to start with the last letter of the previous word:

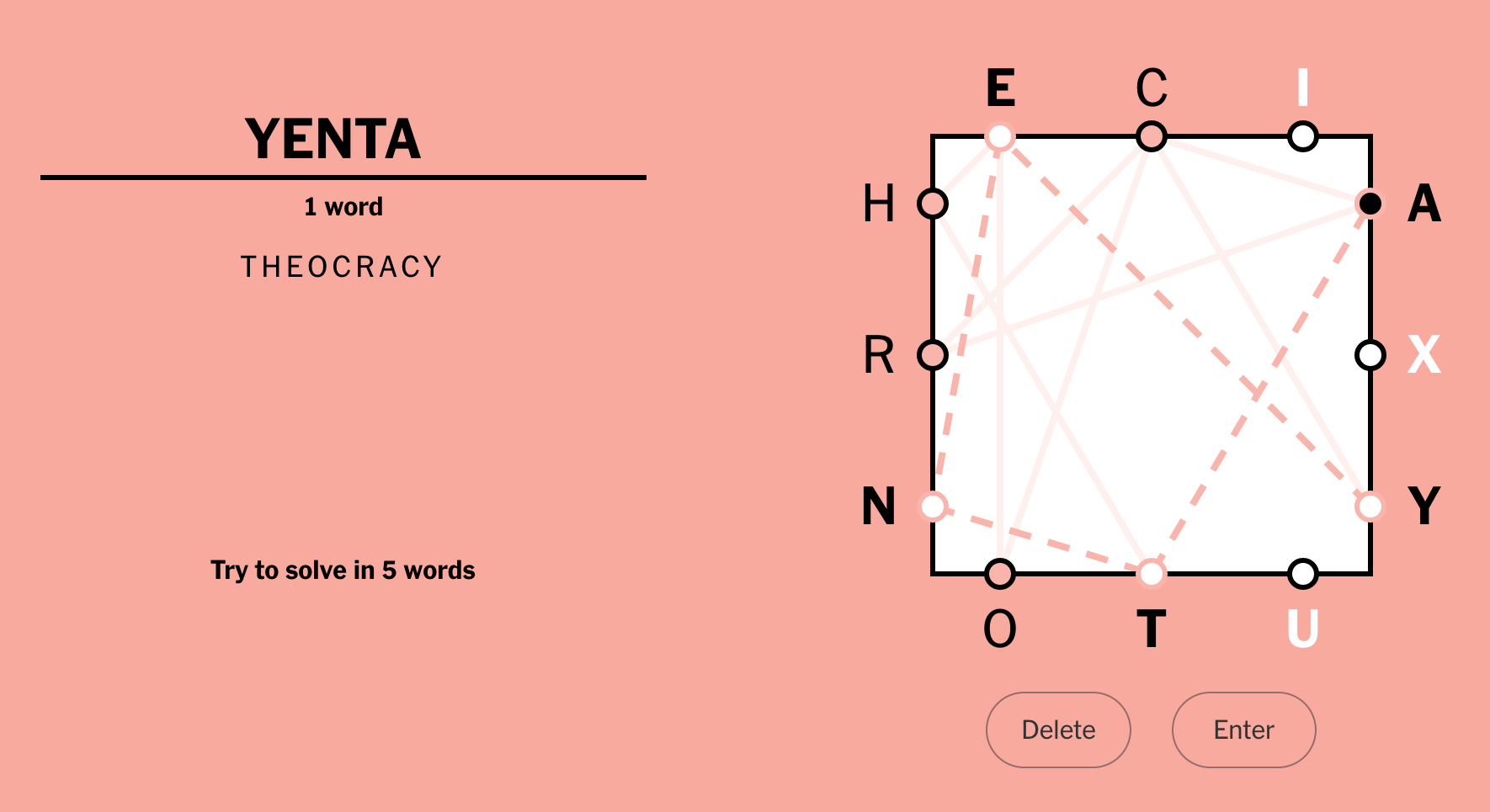
The goal is to use all the letters in a certain number of words. For this puzzle, the challenge is five words.

But if you look at the answers they provide for yesterday’s puzzle, it’s always just two words. So now I’m tormenting myself trying to find two-word solutions. And of course I started thinking about writing a program to find them.

I found a giant list of words and started hacking on some code. I wasn’t sure if I’d need some fancy tree structure for searching the solution space. I figured I would start simpler than that, and maybe it would work.

My strategy was to whittle down the list of words a few steps at a time. First, keep only the words formed from just the 12 letters in the puzzle. Then reduce the list to only those that can be formed following the “not same side” rule. Then find pairs of words that end and start with the same letter, and use all 12 letters:

import collections
import itertools
import sys

def print_sample(label, words, n=10):
    print(f"{label}: {len(words)} words: {', '.join(itertools.islice(words, n))}")

with open("words2.txt") as fwords:
    words = set(w.strip() for w in fwords)

print_sample("All words", words)

sides = sys.argv[1:]
alphabet = set("".join(sides))

words = {w for w in words if set(w) < alphabet}
print_sample("Only the letters", words)

numbered_sides = {c: i for i, side in enumerate(sides) for c in side}

def is_possible(word):
    for first, second in zip(word, word[1:]):
        if numbered_sides[first] == numbered_sides[second]:
            return False
    return True

possible = {w for w in words if is_possible(w)}
print_sample("Possible words", possible)

starts = collections.defaultdict(list)
for word in possible:
    starts[word[0]].append(word)

print("Solutions:")
for word1 in possible:
    last = word1[-1]
    for word2 in starts[last]:
        if set(word1 + word2) == alphabet:
            print(word1, word2)


This code is just stream-of-consciousness coding, intermixing running statements with function I needed. On some previous puzzles, it came up with way too many solutions. For “riu pgh lcs yao” it found 1002 pairs of words! Solutions like “hypacusia argol” are not satisfying...

My giant list of words has 466,551 words. I also have a smaller file with only 45,404 words. I refactored the code to make it more flexible. Now it will try the small word list first, and only go to the second larger list if there are no solutions:

import collections
import itertools
import sys

def print_sample(label, words, n=10):
    print(f"{label}: {len(words)} words: {', '.join(itertools.islice(words, n))}")


class LetterBoxed:
    def __init__(self, sides):
        self.sides = sides
        self.alphabet = set("".join(sides))
        self.numbered_sides = {c: i for i, side in enumerate(self.sides) for c in side}

    def is_possible(self, word):
        for first, second in zip(word, word[1:]):
            if self.numbered_sides[first] == self.numbered_sides[second]:
                return False
        return True

    def solutions(self, words):
        alpha_words = {w for w in words if set(w) < self.alphabet}
        print_sample("Using only the letters", alpha_words)
        possible = {w for w in alpha_words if self.is_possible(w)}
        print_sample("Possible words", possible)

        starts = collections.defaultdict(list)
        for word in possible:
            starts[word[0]].append(word)

        for word1 in possible:
            last = word1[-1]
            for word2 in starts[last]:
                if set(word1 + word2) == self.alphabet:
                    yield (word1, word2)

def main(sides):
    letter_boxed = LetterBoxed(sides)
    for wordfile in ["words.txt", "words2.txt"]:
        with open(wordfile) as fwords:
            words = set(w.strip() for w in fwords)
        print_sample("All words", words)
        solutions = list(letter_boxed.solutions(words))
        if not solutions:
            print("No solutions with these words")
            continue
        print(f"{len(solutions)} solutions:")
        for word1, word2 in solutions:
            print(word1, word2)
        break

if __name__ == "__main__":
    main(sys.argv[1:])


With this, “riu pgh lcs yao” finds five solutions from the short word list, using words I actually know, like “gracious splashy.”

Unfortunately, sometimes the official solution uses words that aren’t in even the enormous word list. A previous puzzle was “tub pxi snq oja”, and the solution offered was “juxtaposition niqab,” which is frustrating. Playing word puzzles inevitably brings you face to face with the differences between accepted word lists.

After I wrote my code, I found:

• Caleb Robinson’s blog post about his solution, which involved the fancier tree structures I avoided.
• Art Steinmetz’s blog post about both generating the puzzle and solving it, in R. He mentions the generalizations of different numbers of sides, and numbers of letters per side. I was amused to realize that my code doesn’t care how many sides or letters per side are used, so it works for any number.

Just for grins, I’m wondering if there’s some crazy way to abuse regexes to do most of the work. Too much time on my hands...

from Planet Python
via read more